NeurIPS Poster, ‘21,
PhysChem: Deep Molecular Representation Learning via Fusing Physical and Chemical Information

Summary

• Used physicist network (PhysNet) and chemist network (ChemNet) simultaneously, and each network shares information to solve individual tasks.
• PhysNet: Neural physical engine. Mimics molecular dynamics to predict conformation.
• ChemNet: Message passing network for chemical & biomedical property prediction.
• Molecule without 3D conformation can be inferred during test time.

Preliminaries

• Molecular representation learning:
  Embedding molecules into latent space for downstream tasks.

• Neural Physical Engines
  Neural networks are capable of learning annotated potentials and forces in particle systems.
  HamNet proposed a neural physical engine that operated on a generalized space, where positions and momentums of atoms were defined as high-dimensional vectors.

• Multi-task learning
  Sharing representations for different but related tasks.

• Model fusion
  Merging different models on identical tasks to improve performance.

Notation

Graph $\mathcal{M} = (\mathcal{V}, \mathcal{E}, n, m, \mathbf{X}^v, \mathbf{X}^e)$

• $\mathcal{V}$: set of $n$ atoms
• $\mathcal{E}$: set of $m$ chemical bonds
• $\mathbf{X}^v \in \mathbb{R}^{n \times d_v} = (x^v_1, …, x^v_n)^\top$: matrix of atomic features
• $\mathbf{X}^e \in \mathbb{R}^{m \times d_e} = (x^e_1, …, x^e_m)^\top$: matrix of bond features

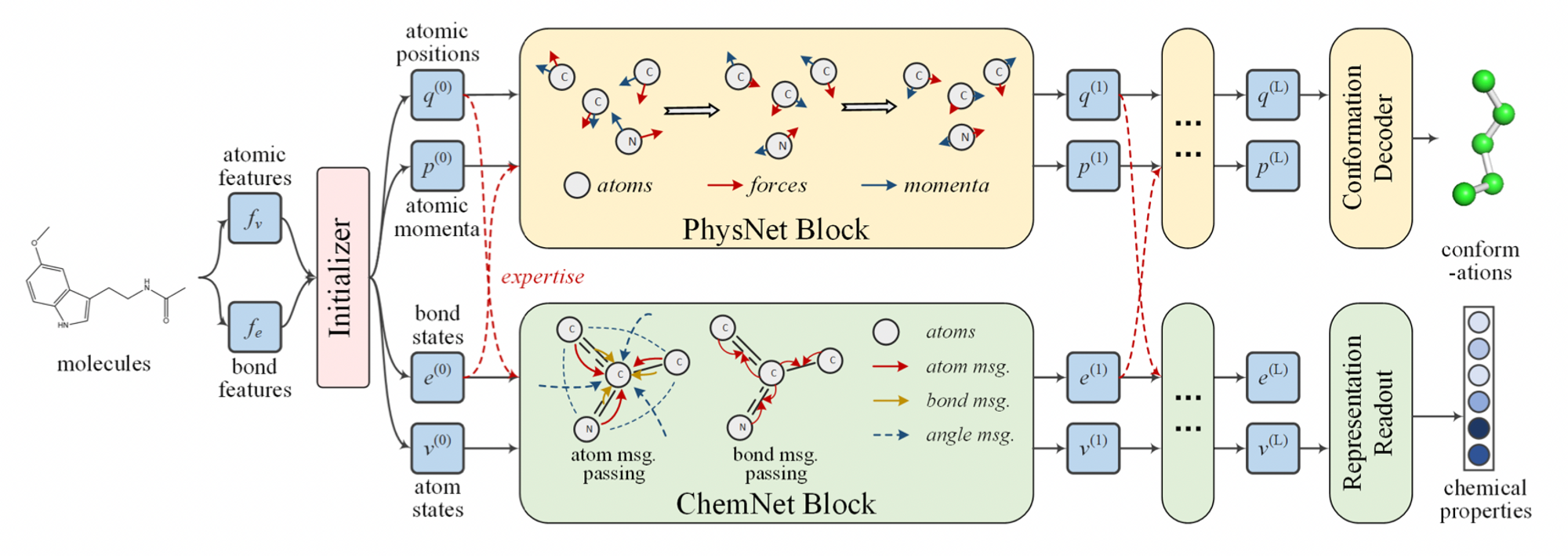
Model

Figure 1. PhysChem Architecture

• Initializer

  • Input: atomic features, bond features (from RDKit)
  • Layer: fully connected layers
  • Output:
  • bond states, atom states for ChemNet
    $v^{(0)}_i = \text{FC}(x^v_i), i\in \mathcal{V}$
    $e^{(0)}_{i,j} = \text{FC}(x^e_{i,j}), (i, j)\in \mathcal{E}$
  • atom positions, atomic momenta for PhysNet
    Bond strength adjacency matrix
    $$A(i,j)=\begin{cases}0, & \text{if $(i,j) \notin \mathcal{E}$} \\ \text{FC}_{\text{sigmoid}}(x^e_{i,j}), & \text{if $(i,j) \in \mathcal{E}$} \end{cases}$$ $\tilde{V} = \text{GCN}(A, V^{(0)})$
    ${ (q^{(0)}_i \oplus p^{(0)}_i)} = \text{LSTM}({\tilde{v}_i}), i \in \mathcal{V}$

• PhysNet

  • PhysNet is inspired by HamNet.
    HamNet showed that neural networks can simulate molecular dynamics for conformation prediction.
  • Directly parameterize the forces between each pair of atoms.
  • Consider the effects of chemical interactions(e.g. bond types) by cooperating with ChemNet’s bond states.
  • Introduces torsion forces.
  • Output: 3D conformation

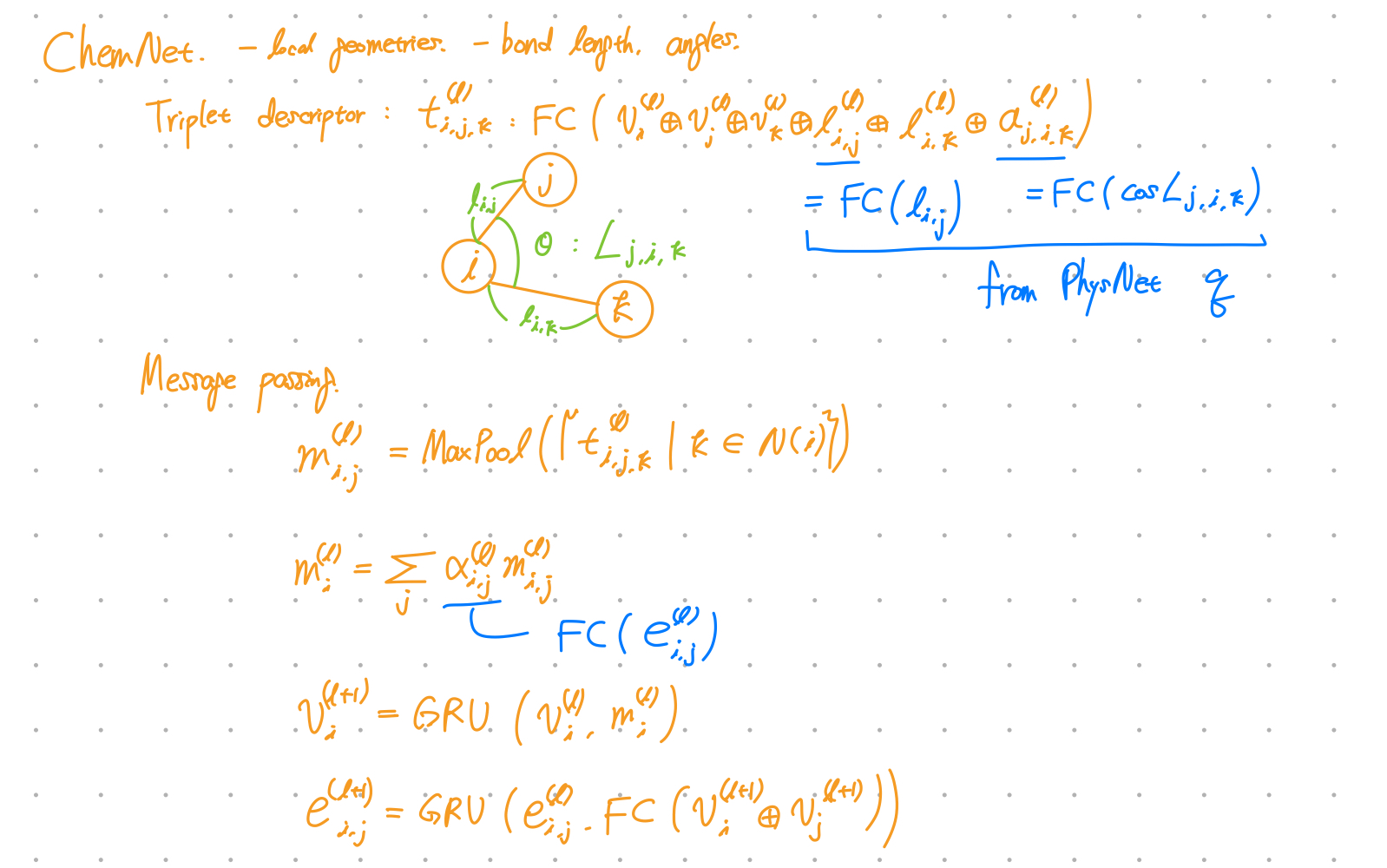
• ChemNet

  • ChemNet modifies MPNN(message passing neural network) for molecular representation learning.
  • Output: Molecule representation

Loss

• $L_{\text{phys}}$: Conn-k loss for Conformation prediction (PhysNet)

  $k$-hop connectivity loss

  $L_{\text{Conn}-k}(\hat{\mathbf{R}}, \mathbf{R}) = |\frac{1}{n} \hat{\mathbf{C}}^{(k)} \odot (\hat{\mathbf{D}} - \mathbf{D}) \odot (\hat{\mathbf{D}} - \mathbf{D}) |_{F}$

  $\odot$: element-wise product

  $| \cdot |$: Frobenius norm

  $(\hat{\mathbf{D}} - \mathbf{D})$ : distance matrix of the real and predicted conformations $(\hat{\mathbf{R}} - \mathbf{R})$

  $\hat{\mathbf{C}}^{(k)}$: normalized $k$-hop connectivity matrix

• $L_{\text{chem}}$: MAE or Cross entropy loss for Property prediction (ChemNet)

• Total loss

  $L_{\text{total}} = \lambda L_{\text{phys}} + L_{\text{chem}}$

Checkpoints

• Is Conn-k loss generally used in other conformation prediction models?

  No! But seems related to local distance loss.

• Is triplet descriptor generally used in other models?

  No!